Another Way to Improve Your Chances In the Enchantments Lottery

Introduction

In previous investigations, I've explored the statistics behind the Enchantments lottery going back to 2021. My curiosity was spurred on by online claims about how people should apply to improve their chances. If you are curious about those articles I suggest reading, Advice on Winning the Enchantment's Lottery (2023 Data Update), in summary:

• Sunday is the best day to apply because you compete against the smallest number of other applicants (along with Tuesday and Wednesday).
• The Colchuck Zone is not a good statistical alternative to the Core Zone.
• Group sizes of one are four times more likely to win than be skipped compared to group sizes of two in the Core Zone.

Similarly, this post looks at another way to "improve" your chances of winning the Enchantments lottery: have multiple people in your group apply.

The Strategy

The Enchantments lottery process only allows applicants to apply once. Additionally, applicants can't even be alternates on other permits. Nor can the winning applicant change their alternate after they've won. This rule blocks a single person from getting their name on more than one permit in the lottery.

However, not every person in the applicant's group is named. As a consequence, in a group of four, each person could apply. This strategy is not new. People do this when trying to win the state and national lotteries. Unlike monetary lotteries, sharing an Enchantments permit is much better than sharing a couple of million dollars. Also, unlike state lotteries, more than one person can win.

The only consequence, or risk, of this method is no one can put another person in the group as an alternate on a permit. That's a pretty substantial risk because it means whoever wins has to go or no one can go.

Hypergeometric Probability Distribution

We can model the probability using the hypergeometric probability distribution if we assume that:

1. Each entry has an equal chance of winning

2. Each entry is randomly selected

3. There are a fixed number of permits awarded each year (2,558 in the year 2023)

Arguably, the way the Enchantments lottery works violates most of these assumptions (the exception being random selection). But, if we pretend we don't know how the lottery works, and we pretend all we know is people who apply for the lottery have a 6.39% winning based on 2023 data then we can calculate some probabilities. You can view the math on the Github repository under the 2023 folder, titled hypergeometric_distribution.ipynb.

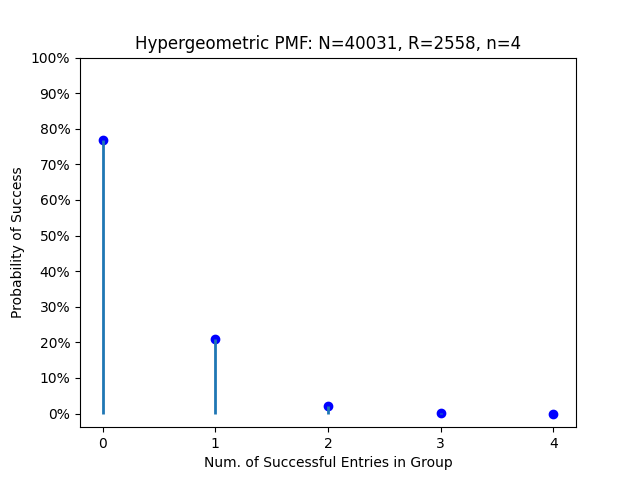
To summarize, if we create a hypergeometric probability distribution composed of a population of 40,031 applicants, of which 2,558 win a permit, with a sample of four applicants, there is a 20.97% that one of the entries is successful.

• Probability of 0 successes in the sample: 76.79%
• Probability of 1 success in the sample: 20.97%
• Probability of 2 successes in the sample: 2.15%
• Probability of 3 successes in the sample: 0.10%
• Probability of 4 successes in the sample: 0.00%

Conclusion

This is a fun exercise—although we made some questionable assumptions—and shows having more people in your group apply for an Enchantments permit increases the odds of winning. Conversely, the strategy comes at the risk of not having an alternate on the permit.